STATS/MATH 425 SEC 007: Introduction to Probability

Fall 2012

Class Information

  1. Days & Time: Tue, Thu 10:00am -- 11:30am
  2. Location: 513 Dennison
  3. Prerequisites: MATH 215 is a formal prerequisite. You should know Calculus (differentiation, integration, change of variables) well.
  4. Description: You will learn basic concepts of probability and become aware of its diverse applications in various scientific and engineering disciplines. The emphasis is on concepts and problem-solving. Topics include axioms of probability, conditional probability, independence, random variables (both discrete and continuous), joint distributions, expectation, variance, covariance.
  5. Textbook: A First Course in Probability (8th edition) by Sheldon Ross.
  6. Ctools: You should access the Ctools class page for this course frequently. It will contain important announcements, posted homework assignments, archive of emails to the class, discussion forum, and chat room.

Instructor Information

Name: Ambuj Tewari

Office: 454 West Hall

Office Hours: Tue, Wed 2:00pm -- 3:30pm, or by appointment

Email: tewaria@umich.edu

GSI information

Name: Jinjing Yang

Office Hours & Location: Wed 1:00pm -- 4:00pm in 274 West Hall

Email: yangjinj@umich.edu

Grading

The final grade in the course will be determined by your scores in homeworks, one midterm exam, and one final exam using the weights given below.

  1. Homeworks (50%): There will be 11 homework assignments in all. I will drop your lowest score and use the remaining 10 assignments to calculate the grade. Late homework submissions will not be accepted unless you present a well-documented case of a medical or family emergency. You are encouraged to discuss problems with your classmates but you should always write up your own solutions. Copying solutions (from anywhere including classmates, internet, previous years’ solutions) is never permitted. Please show all steps in your calculations.
  2. Midterm Exam (20%): This will be a closed-book exam (no notes, no calculator) held in class on Thu, October 18 covering material from chapter 1 through chapter 4, section 4.3 of the book.
  3. Final Exam (30%): This will be a closed-book exam (no notes, no calculator) held in our regular classroom (513 Dennison) on Tue, December 18, 4:00pm -- 6:00pm (as determined by the Office of the Registrar). It will cover material from the entire course.

Accommodations for Students with Disabilities

If you think you need an accommodation for a disability, please let me know at your earliest convenience. Some aspects of this course, the assignments, the in-class activities, and the way the course is usually taught may be modified to facilitate your participation and progress. As soon as you make me aware of your needs, we can work with the Office of Services for Students with Disabilities (SSD) to help us determine appropriate academic accommodations. SSD (734-763-3000; http://www.umich.edu/sswd) typically recommends accommodations through a Verified Individualized Services and Accommodations (VISA) form. Any information you provide is private and confidential and will be treated as such.

Academic Integrity

Please familiarize yourself with the LSA Community Standards of Academic Integrity. The College of LSA expects all of its members to uphold these Standards.

Schedule

The schedule for the semester is given below. References of the form (x.y) refer to sections in the textbook.

Day

Plan

Sep 4

  1. Basic principle of counting (1.2)
  1. Examples 2a, 2c, 2e
  1. Permutations (1.3)
  1. Examples 3b
  2. Self-test 1a, 1b

Sep 6

  1. Permutations contd. (1.3)
  1. Self-test 1c, 1d, 1e, 1f
  1. Combinations (1.4)
  1. Basic formula
  2. Identity (4.1)
  3. Combinatorial proof of Binomial theorem
  4. Example 4e

Sep 11

  1. Multinomial Coefficients (1.5)
  1. Examples 5a, 5b, 5c
  1. Sample space and events (2.2)
  1. Examples of experiments and their sample spaces

Sep 13

  1. Sample space and events (2.2)
  1. Operations (unions, intersections, complements) on events
  2. de Morgan’s laws
  3. Self-test 1
  1. Axioms of probability (2.3)
  1. Examples 3a, 3b
  1. HW 1 out

Sep 18

  1. Inclusion-Exclusion principle (2.4)
  2. Sample spaces having equally likely outcomes (2.5)
  1. Examples 5a, 5b, 5c, 5d

Sep 20

  1. Conditional Probabilities (3.2)
  1. Definition (Eq. (2.1))
  2. Multiplication rule
  3. Examples 2b, 2d
  1. HW 1 due
  1. HW 2 out

Sep 25

  1. Conditional Probabilities (3.2) continued
  1. Example 2h
  1. Bayes’ Formula (3.3)
  1. Examples 3a, parts 1 and 2

Sep 27

  1. Bayes’ Formula (3.3) continued
  1. Examples 3c, 3k
  1. Independent events (3.4)
  1. Examples 4b, 4e
  2. Independence of multiple events
  1. HW 2 due
  2. HW 3 out

Oct 2

  1. Independent Events (3.4) continued
  1. Examples 4g, 4h
  1. Conditional probabilities as ordinary probabilities (3.5)
  1. Random variables (4.1)
  1. Example 1a

Oct 4

  1. Random variables (4.1) continued
  1. Example 1c
  1. Cumulative Distribution Function
  2. Discrete random variables (4.2)
  1. probability mass function
  2. Example 2a
  1. Expected value (4.3)
  1. Examples 3a, 3d
  1. HW 3 due
  1. HW 4 out

Oct 9

  1. Expected value of a function of a random variable (4.4)
  1. Example 4a, Proposition 4.1, Corollary 4.1
  1. Variance (4.5)
  1. Definition, alternative formula
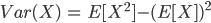
  2. Example 5a
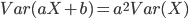
  4. Standard deviation
  1. Bernoulli random variables (4.6)
  1. Eq. (6.1)
  2. Expectation and variance of Bernoulli random variables

Oct 11

  1. Binomial random variables (4.6)
  1. Eq. (6.2)
  2. Example 6b
  3. Expectation and variance (4.6.1)
  4. Computing distribution function (6.4.2)
  1. Poisson random variable (4.7)
  1. Eq. (7.1)
  2. Example 7b
  1. HW 4 due
  1. HW 5 out

Oct 16

NO CLASS (Fall Study Break)

Oct 18

MIDTERM EXAM (10-11:30 in 513 Dennison)

Oct 23

  1. Poisson random variable (4.7) continued
  1. Example 7e
  1. Expected value of sums (4.9)
  1. Proposition 9.1, Corollary 9.2
  2. Example 9d, 9e

Oct 25

  1. Introduction to continuous random variables (5.1)
  2. Expectation and variance (5.2)
  1. Proposition 2.1
  2. Corollary 2.1
  1. The uniform random variable (5.3)
  1. Example 3a
  1. Normal random variables (5.4)
  2. HW 5 due
  1. HW 6 out

Oct 30

  1. Normal random variable (5.4) continued
  1. Examples 4a, 4b
  1. Midterm Student Feedback

Nov 1

  1. Normal approximation to the Binomial (5.4.1)
  1. Example 4f
  1. Exponential random variables (5.5)
  1. Example 5a
  1. HW 6 due
  1. HW 7 out

Nov 6

  1. Exponential random variables (5.5) continued
  1. Examples 5b, 5d
  2. Memoryless property
  1. Hazard rate functions (5.5.1)

Nov 8

  1. Hazard rate functions (5.5.1) continued
  1. Self-test 15a, 15b
  1. Joint distribution functions (6.1)
  1. Example 1a
  1. HW 7 due
  1. HW 8 out

Nov 13

  1. Joint distribution functions (6.1) continued
  1. Examples 1c, 1e
  1. Independent random variables (6.2)

Nov 15

  1. Independent random variables (6.2) continued
  1. Example 2c
  1. Proposition 2.1
  1. Example 2f
  1. HW 8 due
  1. HW 9 out

Nov 20

  1. Sums of independent random variables (6.3)
  1. Formulas (3.1) and (3.2)
  1. Identically distributed uniform random variables (6.3.1)
  1. Example 3a
  1. Normal Random Variables (6.3.3)
  1. Proposition 3.2
  2. Example 3c

Nov 22

NO CLASS (Thanksgiving break)

Nov 27

  1. Poisson and Binomial Random Variables (6.3.4)
  1. Examples 3e, 3f
  1. Conditional distributions: Discrete case (6.4)
  1. Examples 4a, 4b
  1. HW 9 due
  1. HW 10 out

Nov 29

  1. Conditional distributions: Continuous case (6.5)
  1. Examples 5a, 5b
  2. Geometric Random Variable (4.8.1)

Dec 4 (guest lecture by Mr. Sougata Chaudhuri)

  1. Expectation of sums (7.2)
  1. Proposition 2.1, Equation (2.2)
  2. Examples 2a, 2b, 2c, 2f
  3. Example 2i
  1. HW 11 out

Dec 6 (guest lecture by Prof. Stilian Stoev)

  1. Expectation of sums (7.2) continued
  1. Examples 2j, 2n
  1. Moments of number of events (7.3)
  1. Example 3a, 3b, 3d

Dec 11

  1. Covariance, variance of sums, correlations (7.4)
  1. Proposition 4.1, 4.2
  2. Equation (4.1)
  3. Example 4b
  4. Correlation and Equation (4.2)
  5. Example 4d

Dec 13

  1. Extra office hours (in 454 West Hall)
  1. 10-11:30
  2. 2-3:30
  1. HWs 10 and 11 due

Dec 18

FINAL EXAM (4-6 in 513 Dennison)